Relative dimension

In mathematics, specifically linear algebra and geometry, relative dimension is the dual notion to codimension.

In linear algebra, given a quotient map 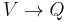, the difference dim V − dim Q is the relative dimension; this equals the dimension of the kernel.

In fiber bundles, the relative dimension of the map is the dimension of the fiber.

More abstractly, the codimension of a map is the dimension of the cokernel, while the relative dimension of a map is the dimension of the kernel.

These are dual in that the inclusion of a subspace 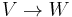of codimension k dualizes to yield a quotient map 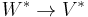of relative dimension k, and conversely.

The additivity of codimension under intersection corresponds to the additivity of relative dimension in a fiber product.

Just as codimension is mostly used for injective maps, relative dimension is mostly used for surjective maps.